
분산(variance) : 편차 제곱의 합을 자료의 수로 나눈 값
왜 n이 아니라 n-1로 나누는걸까?
통계량을 구하는 이유는 모수 추정이며 통계량은 최대한 모수에 가까워야한다.
좋은 통계량을 구하는 기준 중 하나인 불편성(unbiasedness)는 편향이 없음을 의미한다.
불편성을 만족하는 불편 통계량을 쓰는 공식이 위의 분산 공식이며 n-1로 나누는 이유이다.
모집단에 대한 분산을 구할 경우에는 n-1이 아닌 n으로 나눈다.
표준편차(standard deviation) : 분산을 제곱근한 값
표본 표준편차의 경우 n-1로 나누며, 모표준편차일 경우 n으로 나눈다.
데이터 샘플링 후 표본 데이터에 대하여 통계량을 구하기 때문에 대부분의 경우에는
n-1로 나누는것이 불편성이라는 성질을 만족하는 통계량을 생성한다.
분산을 제곱근하는 이유는 무엇일까?
평균으로부터 데이터가 얼마나 떨어져 있는지를 구했는데 스케일이 달라졌기 때문에 제곱된 것에 대해 제곱근으로 상쇄한다.
이런 이유로 분산보다 분산을 제곱근한 표준편차가 더 많이 사용된다.
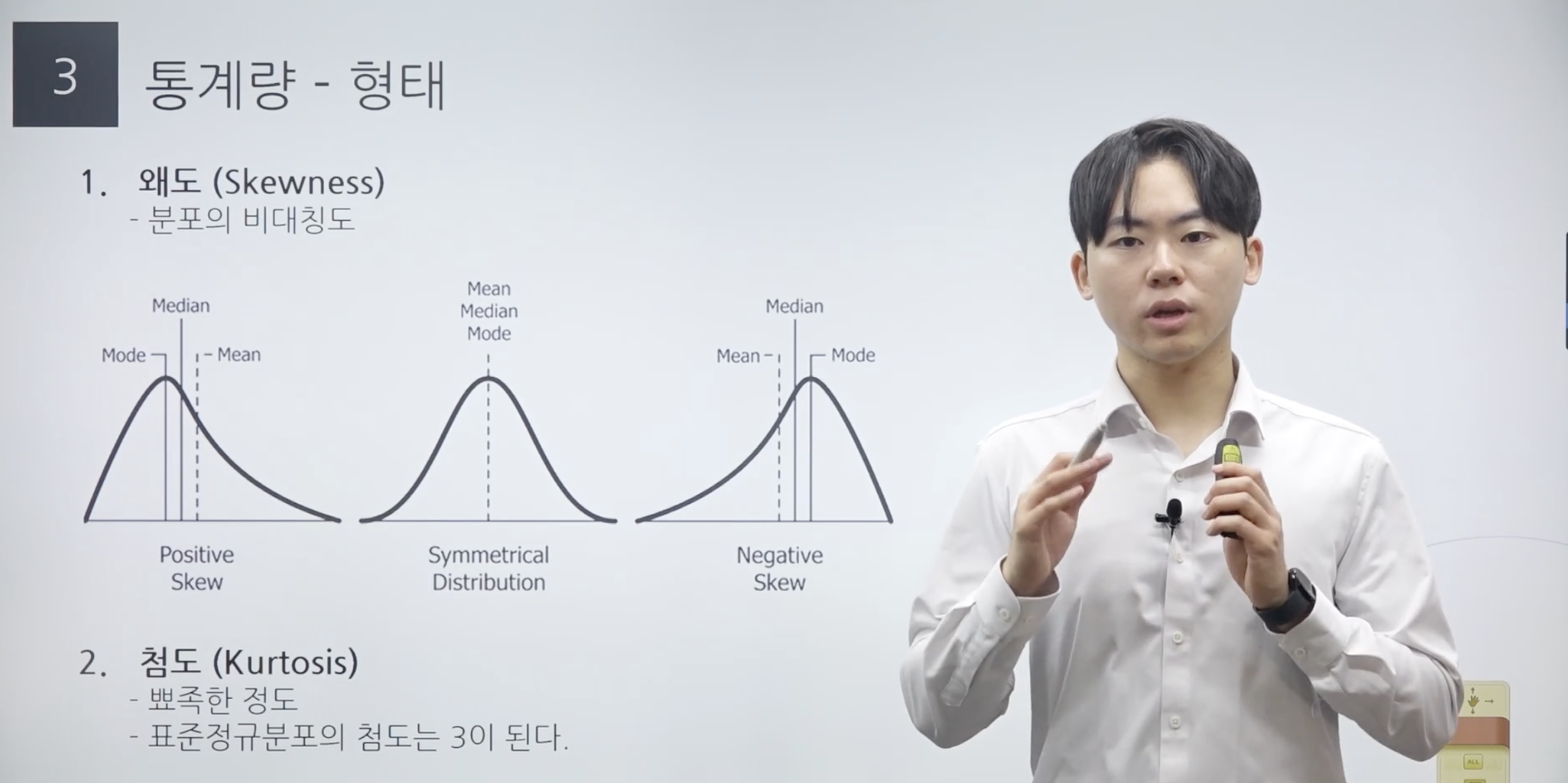
왜도(skewness) : 분포의 비대칭도
왜도가 0일 경우 분포가 가운데를 기준으로 정확하게 일치하며 mode, median, mean이 정확하게 일치한다.
왜도가 음수일 경우 왼쪽으로 꼬리가 길어진 형태
왜도가 음수일 경우 오른쪽으로 꼬리가 길어진 형태
왜도가 양일 때 mode < median < mean 의 형태를 취하며
왜도가 양이라는 것은 양의 값 중에 분포에서 떨어진 값들이 존재한다는 것을 의미한다.
극단값이 존재한다는 것은 평균 연산에 영향을 미치는 것을 의미하며 그렇기 때문에 왜도가 양일 때 평균(mean)의 크기가 가장 크다.
첨도(kurtosis) : 뾰족한 정도
표준정규분포의 첨도는 3이다.

상관(correlation) : 확률변수 X, Y의 변화가 서로 관계가 있을 때 상관관계가 있으며, 선형적 관련성을 파악함
X, Y에 대하여 X가 증가할 때 Y도 증가하거나 감소할 때 그 방향이 일정한 것을 선형적 연관성이라고 한다.
예를 들어 키와 성적으로 X, Y를 정한 경우 분포에 규칙이 존재할 수 있다. 하지만 이는 비선형적 관련성으로 분류한다.
이를 고려하지 않고 선형적 관련성만 파악하는 상관계수로 데이터에 대한 수치적인 요약을 할 경우 오류가 발생될 수 있다.
공분산(covariance)
모 공분산은 n-1대신 n으로 나누어 주면 된다.

상관계수(correlation coefficient) : 공분산을 두 변수의 표준편차의 곱으로 나눈 값
상관계수를 구하는 공식은 표본 공분산을 x, y 각각의 표본 표준편차로 곱한것으로 나누어진 것이다.
상관계수 r : -1 <= r <= 1
공분산은 데이터의 단위에 따라 값이 달라지지만 상관계수는 -1부터 1까지의 값으로 가둬둔다.
두 양적 변수간의 선형적 연관성의 강도를 측정한다.
단위가 없다.
절댓값이 1에 가까울수록 연관성의 강도가 높아진다. (강도가 낮은것은 0, 음수일 경우에도 절댓값이 1에 가깝다면 높은 강도를 의미한다.)

상관계수 r 은 x, y의 공분산을 x, y의 표준편차의 곱으로 나누어준 값이다. 공식을 적용하면 분모 (n-1)이 모두 약분되어 상관계수를 구하는 것이 가능하다.
위 내용은 메타코드 "통계 기초의 모든것 올인원"강의의 1편 1강 : 통계량의 "산포", "형태", "상관"의 요약 내용입니다.
아래 링크를 통해 통계 기초 강의 수강이 가능합니다.
https://metacodes.co.kr/edu/read2.nx?M2_IDX=31635&EP_IDX=8382&EM_IDX=8208
통계 기초의 모든것 올인원 [ 1편, 2편 ]ㅣ18만 조회수 검증
metacodes.co.kr
메타코드 사이트 내에서 통계 기초뿐만 아니라 다양한 강의 수강이 가능하며 다양한 이벤트 참여와 현직자 특강 수강이 가능합니다.
해당 게시물은 서포터즈 지원을 받아 작성하였습니다.
'수학' 카테고리의 다른 글
| [메타코드 강의후기] 통계 기초의 모든것 | 확률과 확률변수(3) (1) | 2024.07.01 |
|---|---|
| [메타코드 강의후기] 통계 기초의 모든것 | 확률과 확률변수(2) (0) | 2024.06.23 |
| [메타코드 강의후기] 통계 기초의 모든것 | 확률과 확률변수(1) (0) | 2024.06.20 |
| [메타코드 강의후기] 통계 기초의 모든것 | 통계량(1) (0) | 2024.06.17 |
| 빈도주의와 베이지안 (0) | 2023.10.20 |